시간복잡도
- 알고리즘의 성능을 나타내는 지표
- 입력 크기에 대한 연산 횟수의 상한을 의미
- 시간복잡도는 낮으면 낮을 수록 좋음
- 모든 알고리즘은 입력되는 데이터의 크기 또는 갯수에 따라 이의 계산 횟수 수행 시간이 크게 달라지게 된다
- 입력받은 데이터의 크기에 따른 알고리즘의 수행시간의 변화가 시간복잡도
- 시간복잡도가 더 큰 알고리즘들은 더 큰, 혹은 많은 데이터를 처리할 때 훨씬 더 오랜 시간이 걸리게 되지만
- 계산횟수의 정확한 측정이 어렵기 때문에, 보통 Big O 표기법이라는 것을 이용해 표시
Big O 표기법
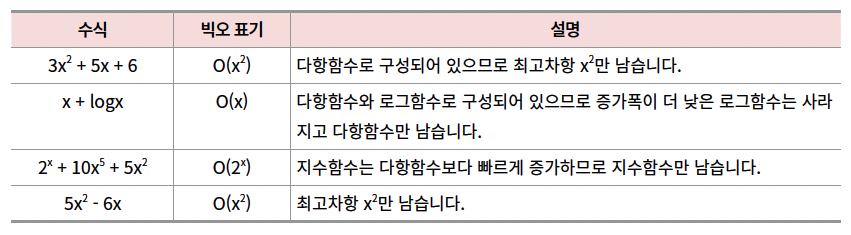
2n+7번 계산하는 알고리즘일 때 n이 커지면 2n과 사실상 차이가 없다
그러므로
O(2n+7) = O(2n)
대략 O표기법은 상수만큼의 시간 차이는 무시하는 것이다
계산 횟수에 붙은 상수는 별로 중요하지 않다
n이 커지면 n이 커짐에 따라 증가하는 계산횟수가 훨씬 더 중요해지기 때문에
시간복잡도를 나타낼 때는 상수를 모두 제거한다
n, 8n+100, 12234n 은 모두 O(n)
이러한 이유로
3^n + 2*n^3 + n^2는 시간 복잡도 O(3^n) 으로 나타낼 수 있다,
| 시간 복잡도 | 설명 |
| O(1) | 상수 형태. n의 값에 상관없이 일정한 양의 계산만 한다 |
| O(log n) | 로그 형태 |
| O(n) | 선형 |
| O(n log n) | 선형 로그 형태 |
| O(n^2), O(n^3) | 다차 형태 |
| O(2^n) | 지수 형태 |
| O(n!) | 팩토리얼 형태 |

연산 횟수는 1,000~3,000만 정도로 고려해서 시간 복잡도를 생각하기
예제
별 그리기 문제
N=3이면
*
**
***
일때 연산횟수는 1+2+3=6 시간복잡도 O (N^2)
식으로 표현할땐 N(N+1)/2
박테리아 수명문제
초기 박테리아 세포 개수가 N일 때 해마다 세포 개수가 이전 세포 개수의 반으로 준다면 언제 모든 박테리아가 죽을지 계산하기


(½)^Y * N <= 1인 결과를 찾기
해당 시간 복잡도 O(logN)
'CS > 알고리즘' 카테고리의 다른 글
| 기본 정렬 알고리즘 O(n^2) (0) | 2024.07.30 |
|---|---|
| 자료 구조 - 비선형 자료 구조 (트리) (0) | 2024.07.29 |
| 자료 구조 - 비선형 자료 구조 (그래프) (0) | 2024.07.29 |
| 선형 구조 자료 탐색법 (0) | 2024.07.29 |
| 자료 구조 - 선형 자료 구조 (0) | 2024.07.29 |
